在使用神经网络时,我们要加入非线性的函数,这样神经网络学到的 “边界” 才会更加的精确、光滑,神经网络的 “黑箱” 才可以表示更多复杂的函数来解决更加复杂的问题。
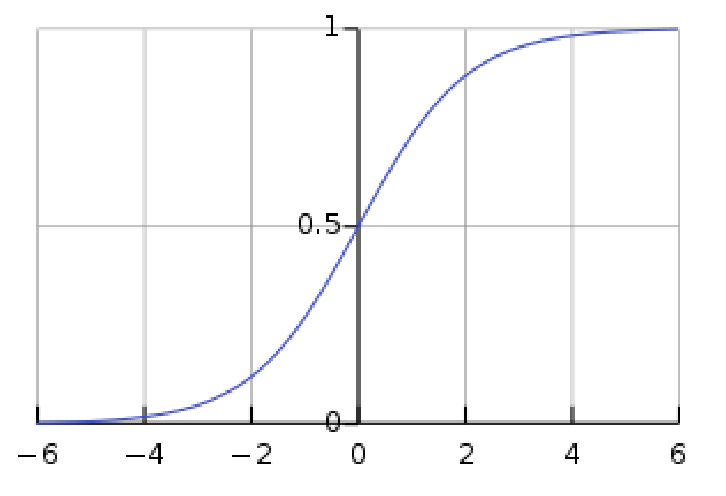
Sigmoid 激活函数。我们知道在做二分类时我们经常使用sigmoid函数,它可以表示 P(y=1|x) 的概率,但是我们基本只在输出层使用它,几乎不在神经网络中间使用它,是因为如下图,如果输入落在0附近,梯度是相当大的,我们迭代weights时一般使用Backpropagation,根据求导的链式法则,由于神经网络层数一层层叠加,就会出现梯度爆炸的问题,一般我们使用梯度裁剪即Gradient Clipping来解决梯度爆炸问题;而如果输入不落在中间区间,sigmoid函数saturate,saturated neurons kill the gradient flow,梯度逐渐趋近于0,这时候会出现梯度消失问题,对于梯度消失问题我们可以使用ReLU函数来解决。而且Sigmoid 函数输出一直是positive的,s = sigmoid(f(x))其中f(x)=wx+b, 对w求导根据链式法则我们可以得到
前一项大于0,而x大于零或者小于0,就使得在梯度下降迭代weights时,it is going to be either positive or negative for all weights, 这时候梯度下降的路线会出现Zig Zag path,使得优化过程变得缓慢,原本可以一步到位的可能多出好多倍的时间。
优:可以很好的表示概率P(y=1|x)
缺:梯度爆炸;梯度消失; Zig Zag path
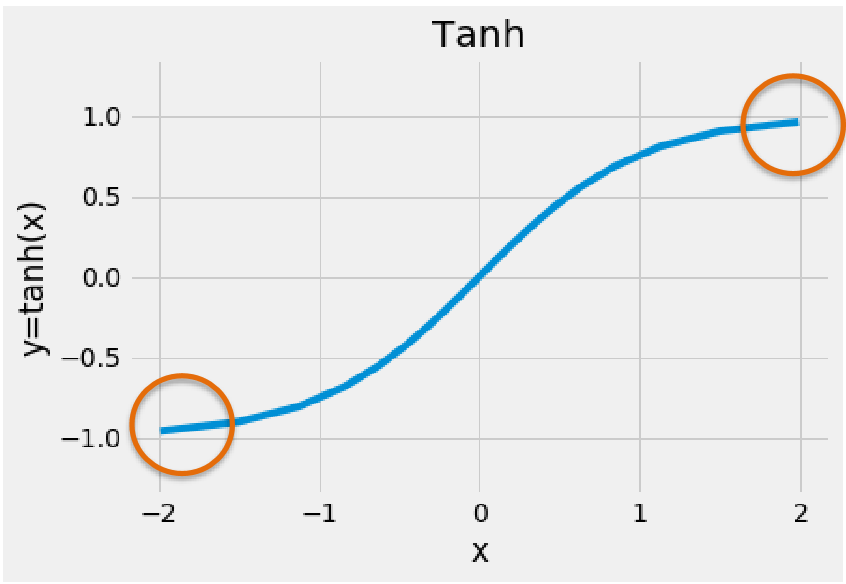
Tanh 激活函数。 类似于sigmoid的函数,在sigmoid基础上变为zero-centered,更容易被优化,但是梯度爆炸以及消失的缺点仍然存在。
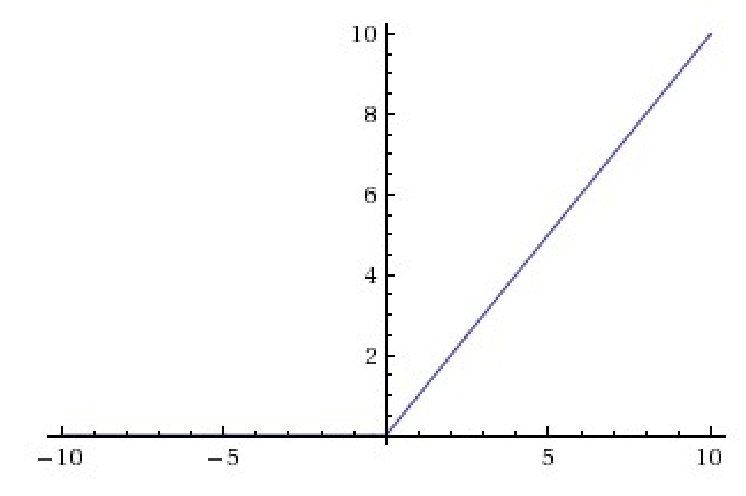
ReLU 激活函数。ReLU函数由于梯度在第一象限恒为1,所以可以很好解决梯度消失的问题,并且由于梯度为一个constant,所以使用梯度下降时间以及空间复杂度会十分低,但是由于在输入为负时,梯度会负,这时候会有死亡ReLU的问题。
- 优:避免梯度消失;时间空间复杂度更低
- 缺:无法避免梯度爆炸;死亡ReLU
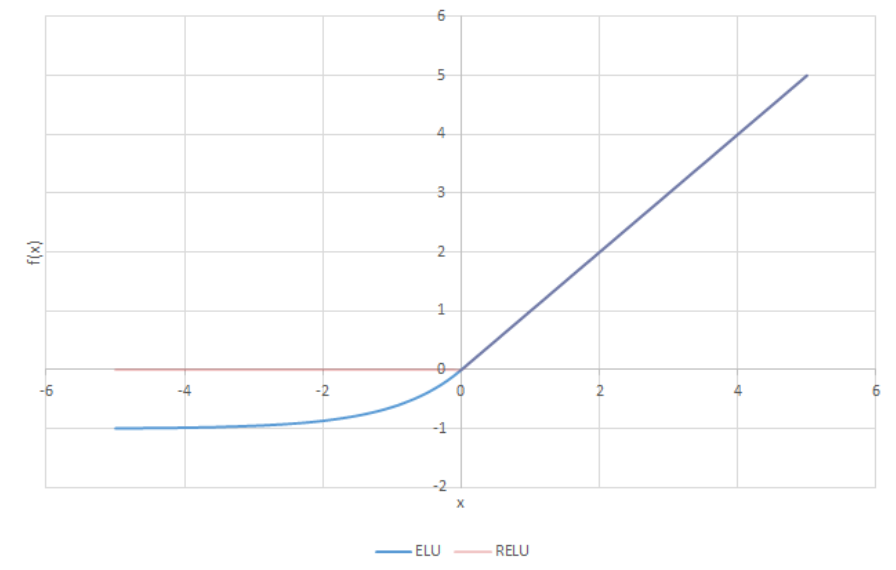
ELU 激活函数。在ReLU基础上让其在输入为负时梯度不为0,但是由于引入指数运算,计算复杂度会大大上升,并且α是一个hyper parameter,不能被学习到,会影响神经网络的性能。
- 优:继承ReLU优点,避免死亡ReLU的问题
- 缺:无法避免梯度爆炸;指数运算复杂;引入新的hyper parameter
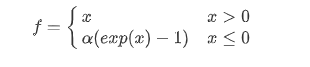
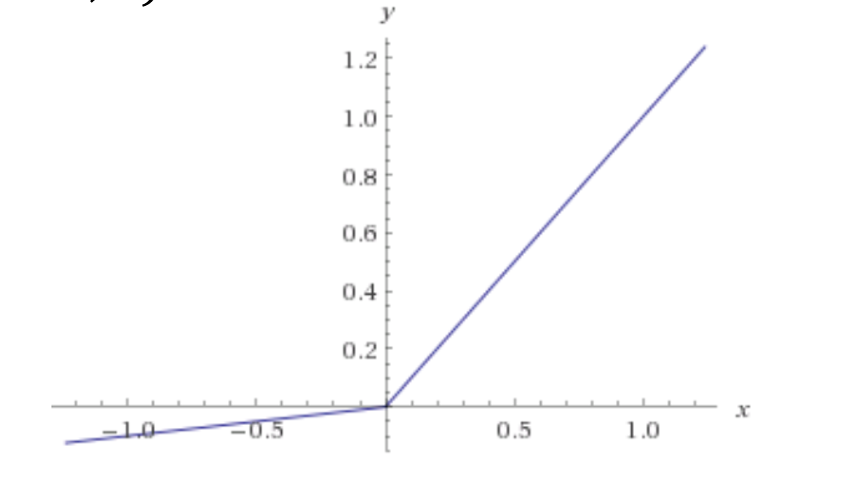
Leaky ReLU激活函数。相比ELU,无指数运算,大大降低计算复杂度,但是由于正负时均为线性函数,所以相比ELU,有一些局限性
- 优:继承ELU优点;无指数运算,计算复杂度大大下降
- 缺:无法避免梯度爆炸;相比ELU,由于正负部分均为线性,有一定局限性;引入了一个新的hyper parameter
f(x) = max(αx,x)
SELU 激活函数。收敛快,不会出现梯度爆炸或者消失问题(internal normalization), 但是对初始化有特殊要求(initialization function lecun_normal)。
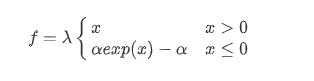
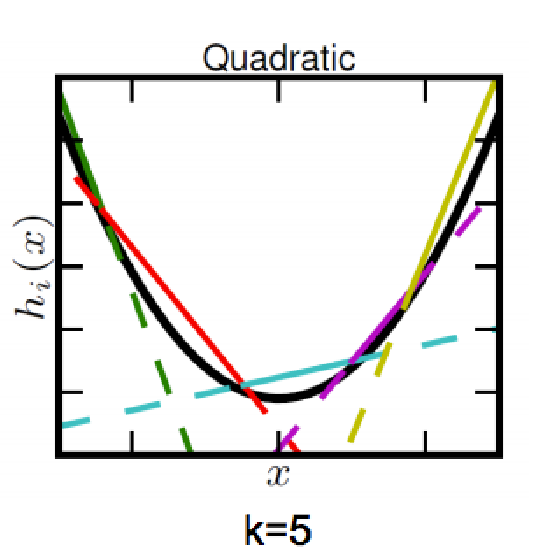
Maxout Units。注意是很多个Units共同组成(数目不定)。多个线性的分界线可以去逼近一个convex function。个数越多,越逼近
- 优:不会死;不会saturate;Linear Regimes;Generalization of ReLUs
- 缺:会大大增加参数量
一些激活函数使用建议:
- Sigmoid 函数一般真的不用:)
- ReLU是最普遍使用的激活函数
- 除了ReLU的第二选择是ReLU的变种(ELU,Leaky ReLU等等)或者Maxout激活函数
- Recurrent nets需要使用tanh或者相似的函数